Sorry, you need an SVG-compatible browser to view the interactive version.
Everyone is always raving about bloom filters. But what exactly are they, and what are they useful for?
The basic bloom filter supports two operations: test and add.
Test is used to check whether a given element is in the set or not. If it returns:
Add simply adds an element to the set. Removal is impossible without introducing false negatives, but extensions to the bloom filter are possible that allow removal e.g. counting filters.
The classic example is using bloom filters to reduce expensive disk (or network) lookups for non-existent keys.
If the element is not in the bloom filter, then we know for sure we don't need to perform the expensive lookup. On the other hand, if it is in the bloom filter, we perform the lookup, and we can expect it to fail some proportion of the time (the false positive rate).
I wrote a very fast bloom filter implementation in JavaScript called bloomfilter.js. It uses the non-cryptographic Fowler–Noll–Vo hash function for speed. We can get away with using a non-cryptographic hash function as we only care about having a uniform distribution of hashes.
The implementation also uses JavaScript typed arrays if possible, as these are faster when performing low-level bitwise operations.
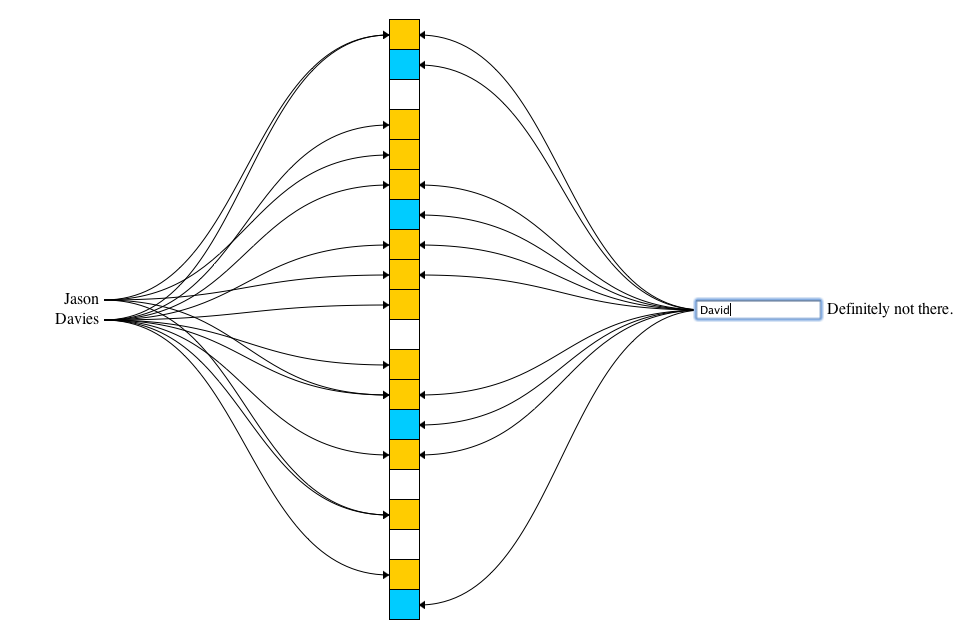
Below you should see an interactive visualisation of a bloom filter, powered by bloomfilter.js.
You can add any number of elements (keys) to the filter by typing in the textbox and clicking "Add". Then use the second textbox to see if an element is probably there or definitely not!

Sorry, you need an SVG-compatible browser to view the interactive version.
The bloom filter essentially consists of a bit vector of length m, represented by the central column.
To add an item to the bloom filter, we feed it to k different hash functions and set the bits at the resulting positions. In this example, I've set m to 50 and k to 3. Note that sometimes the hash functions produce overlapping positions, so less than k positions may be set.
To test if an item is in the filter, again we feed it to the k hash functions. This time, we check to see if any of the bits at these positions are not set. If any are not set, it means the item is definitely not in the set. Otherwise, it is probably in the set.
Astute readers will note that I only mentioned one hash function, Fowler–Noll–Vo, but bloom filters require several. It turns out that you can produce k hash functions using only two to start off with. In fact, I just perform an additional round of FNV as the second hash function, and this works great. Unfortunately I can't use the 64-bit trick in the linked post as JavaScript only supports bitwise operations on 32 bits.