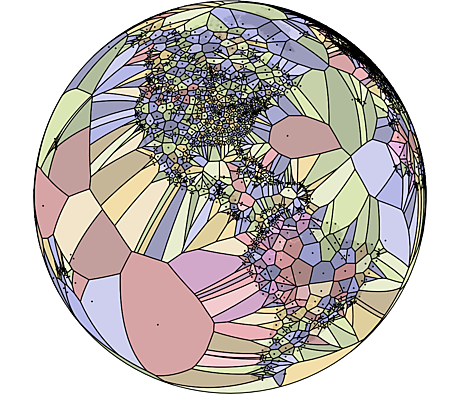
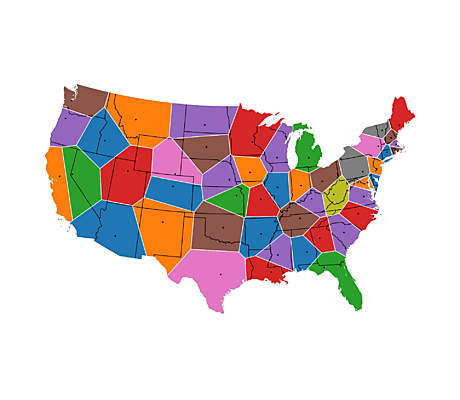
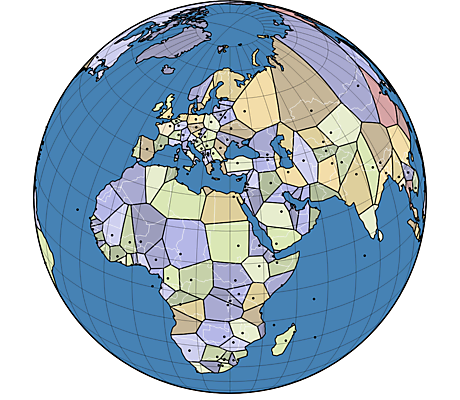
A Voronoi diagram for a set of seed points divides space into a number of regions. There is one region for each seed, consisting of all points closer to that seed than any other. In this case, the space is the surface of the globe (approximated as a sphere).
This implementation uses a randomised incremental algorithm to compute the 3D convex hull of the spherical points. The 3D convex hull of the spherical points is equivalent to the spherical Delaunay triangulation of these points.
A work in progess! Remaining items:
- Handle coplanar points correctly.
- Show the spherical convex hull (this is the boundary of the Delaunay triangulation for points ⊆ hemisphere, otherwise the whole sphere).